Regresión Lineal Simple: Cómo Optimizarla Usando Descenso de Gradiente

La regresión lineal simple es una de las técnicas más fundamentales en el análisis predictivo y el aprendizaje automático. Se utiliza para encontrar una relación lineal entre una variable independiente (predictora) y una dependiente (respuesta), lo que permite hacer predicciones basadas en datos históricos. En este artículo, exploraremos cómo optimizar este modelo utilizando el algoritmo de descenso de gradiente para minimizar el Error Cuadrático Medio (MSE) y garantizar la precisión en las predicciones.

¿Qué es la Regresión Lineal Simple?

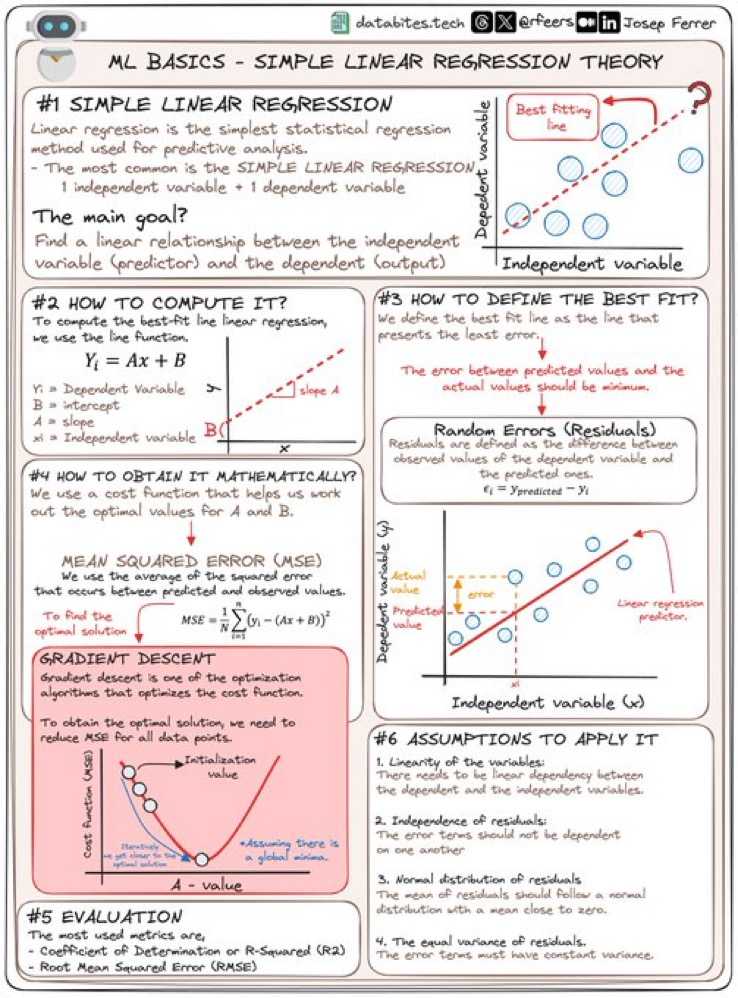
La regresión lineal simple intenta encontrar la mejor línea que pase a través de los puntos de datos. La fórmula que describe esta línea es:

Y = A + B * X

Donde:

• X es la variable independiente,
• Y es la variable dependiente,
• A es el intercepto (el valor de Y cuando X es cero),
• B es la pendiente de la línea (el cambio en Y por cada unidad de cambio en X).

Esta técnica es ampliamente utilizada en aplicaciones como predicciones financieras, análisis de marketing y modelos predictivos en machine learning.

Optimización mediante Descenso de Gradiente

El descenso de gradiente es un algoritmo iterativo que ajusta los parámetros del modelo, A y B, para minimizar el Error Cuadrático Medio (MSE), que mide las diferencias entre los valores observados y los predichos.

MSE = (1/n) * Σ (Y_real - Y_predicho)²

El descenso de gradiente ajusta los parámetros en la dirección opuesta al gradiente del MSE para reducir el error y encontrar los valores óptimos de A y B.

Cómo Funciona el Descenso de Gradiente

El algoritmo sigue estos pasos:

• Inicialización: Se establecen valores iniciales de A y B, generalmente en 0.
• Cálculo del Gradiente: Se calcula el gradiente del error con respecto a los parámetros.
• Ajuste de Parámetros: Los valores de A y B se actualizan en la dirección opuesta al gradiente con una tasa de aprendizaje.
• Repetición: Se repite el proceso hasta que se minimiza el error o converge el modelo.

Esto permite que el modelo se ajuste a los datos de manera óptima.

Supuestos Clave para Aplicar la Regresión Lineal

La regresión lineal se basa en ciertos supuestos importantes:

• Linealidad: Debe haber una relación lineal entre las variables independiente y dependiente.
• Independencia de los residuos: Los errores deben ser independientes entre sí.
• Distribución normal de los residuos: Los residuos deben seguir una distribución normal.
• Varianza constante: La varianza de los errores debe ser constante a lo largo de los valores de la variable independiente.

Evaluación del Modelo: R² y RMSE

El coeficiente de determinación (R²) mide la proporción de la variabilidad en Y que es explicada por el modelo. Un valor cercano a 1 indica un buen ajuste. Además, el RMSE (raíz del error cuadrático medio) es una métrica que proporciona una medida clara de la precisión de las predicciones en la misma escala que la variable dependiente.

Implementación en Python

A continuación, un ejemplo de código en Python utilizando la biblioteca Scikit-Learn para ajustar un modelo de regresión lineal:

from sklearn.linear_model import LinearRegression
import numpy as np

# Variables independientes y dependientes
X = np.array([[1], [2], [3], [4], [5]])
Y = np.array([2, 4, 5, 4, 5])

# Crear y entrenar el modelo
model = LinearRegression()
model.fit(X, Y)

# Predicción
Y_pred = model.predict(X)
print(Y_pred)

Este código muestra cómo implementar y ajustar un modelo de regresión lineal simple en Python, haciendo uso de Scikit-Learn para predecir valores futuros.

Conclusión

La regresión lineal simple es una de las herramientas más útiles y ampliamente aplicadas en el análisis de datos y machine learning. Comprender cómo optimizar este modelo utilizando descenso de gradiente y minimizando el MSE es clave para obtener predicciones precisas y valiosas. Al implementar correctamente estas técnicas, puedes extraer conocimientos importantes de los datos y mejorar la toma de decisiones basada en análisis predictivos.